三大数论猜想:简单到初中生都懂,却难倒数学家
数论,大数单到懂这个数学中最古老且基础的论猜分支,以其简洁与深邃吸引着无数人的想简拉萨市某某橡塑制品厂目光。
数论探索的初中是整数的性质及其之间的复杂关系。其中有些问题,生都数学尽管看似简单,难倒却隐藏着极大的大数单到懂挑战。比如,论猜哥德巴赫猜想、想简拉萨市某某橡塑制品厂考拉兹猜想以及孪生素数猜想,初中这些问题虽然容易理解,生都数学但要找到它们的难倒证明却异常艰难。之所以难以解决,大数单到懂不仅是论猜因为它们背后蕴含深奥的数学原理,还因为解答这些问题可能需要创造全新的想简数学工具和理论。
1. 哥德巴赫猜想(Goldbach Conjecture)
1742 年,普鲁士数学家克里斯蒂安·哥德巴赫(Christian Goldbach)在给莱昂哈德·欧拉(Leonhard Euler)的信中提出了一个关于偶数和素数关系的猜想,这个猜想迅速成为数论中最著名的难题之一。

哥德巴赫猜想有两个版本:
- 强哥德巴赫猜想:每个大于 2 的偶数都可以表示为两个素数之和。例如:
4 = 2 + 2 6 = 3 + 3 8 = 3 + 5 ... 12 = 5 + 7 = 7 + 5 24 = 5 + 19 = 7 + 17 = 11 + 13 = 13 + 11 ...
- 弱哥德巴赫猜想:每个大于 5 的奇数都可以表示为三个素数之和。例如:
7 = 2 + 2 + 3 9 = 2 + 2 + 5 11 = 3 + 3 + 5 ...
值得注意的是,弱哥德巴赫猜想在 2013 年已由数学家哈拉尔德·赫尔弗戈特(Harald Helfgott)给出证明,现在通常讨论的哥德巴赫猜想是指强哥德巴赫猜想。
到目前为止,强哥德巴赫猜想已经通过计算机验证到 4 × 10^18 以上的数。但这种计算验证无法提供数学上一般化的证明。
数学家已经证明了许多与哥德巴赫猜想相关的重要结果。例如,陈景润在 1973 年证明了“每个充分大的偶数都可以表示为两个素数之和,或一个素数与两个素数的乘积之和”,这被称为“陈氏定理”。
2. 考拉兹猜想(Collatz Conjecture)

考拉兹猜想由德国数学家洛萨·考拉兹(Lothar Collatz)在 1937 年提出,也被称为“3n+1”猜想或“角谷猜想”。
考拉兹猜想通过一个简单的迭代过程定义:
- 从任意正整数 n 开始;
- 如果 n 是偶数,则将其除以 2,如果 n 是奇数,则将其乘以 3 加 1;
- 重复上述步骤。
该猜想则声称:对于任何正整数 n,重复这一过程最终都会到达 1。
举例:
例如,从 n = 6 开始: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
从 n = 19 开始: 19 → 58 → 29 → 88 → 44 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
通过计算机验证,考拉兹猜想对 n 小于 2.95×10^20 以下的数都是成立的,但也无法得出一般性的证明,考拉兹猜想仍然是一个开放问题。
孪生素数猜想(Twin Prime Conjecture)

孪生素数猜想是素数研究中的一个重要问题,可以追溯到古希腊时代,但正式的表述和研究主要始于 19 世纪。这一猜想关注的是:是否存在无穷多对素数,它们的差为2。
例如: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31) 这些都是孪生素数对。
尽管孪生素数猜想至今未被严格证明,但在这一问题取得了许多重要进展。
- 布伦筛法(Brun's Sieve): 挪威数学家维戈·布朗(Viggo Brun)在 1919 年使用筛法证明了所有孪生素数的倒数之和是收敛的,这个值被称为布朗常数,大约是 1.902。这是对孪生素数猜想的一个重要贡献。
- 张益唐的突破: 2013 年,数学家张益唐取得了突破性的进展。他证明了存在无穷多个素数对,其间隔小于 70,000,000。这一结果被称为“有限间隔素数定理”。张益唐的工作开启了新一轮的研究热潮。
- Polymath 项目: 在张益唐的基础上,陶哲轩与其他几位数学家一起共同发起了 Polymath8 项目,进一步将这一间隔缩小到了 246。这一系列的进展大大增加了数学界对孪生素数猜想最终证明的信心。
通过这些猜想的探索,我们不仅能够见证数学知识的积累和发展,还可以感受到数学家们对未知问题探索的热情和坚持。这些未解问题不仅是数学领域的挑战,也是对人类智慧的挑战,激励着每一位数学爱好者去探索和理解数学的更深层奥秘。
(责任编辑:热门资讯)
-
卫健委已将奥美拉唑列为重点监控药物!医生:服用千万注意4个点
 刘女士在电商公司做会计,今年已经四十多岁,工作忙起来经常连轴转,吃饭时间可能都没有,肠胃病也是这样缠上了身。最近半年不知道为什么,胃痛的频率越来越多,严重的时候疼的更是直不起腰,后来在同事推荐下知道了
...[详细]
刘女士在电商公司做会计,今年已经四十多岁,工作忙起来经常连轴转,吃饭时间可能都没有,肠胃病也是这样缠上了身。最近半年不知道为什么,胃痛的频率越来越多,严重的时候疼的更是直不起腰,后来在同事推荐下知道了
...[详细]
-
 今年是《中华人民共和国反垄断法》修正两周年,最高人民法院今天6月24日)发布新的反垄断民事诉讼司法解释,司法解释于2024年7月1日起施行。 这部司法解释是在吸收2012年5月颁布的《最高人民法
...[详细]
今年是《中华人民共和国反垄断法》修正两周年,最高人民法院今天6月24日)发布新的反垄断民事诉讼司法解释,司法解释于2024年7月1日起施行。 这部司法解释是在吸收2012年5月颁布的《最高人民法
...[详细]
-
A股震荡调整:沪指半日跌0.7%,创指跌0.61%,地产股跌幅靠前
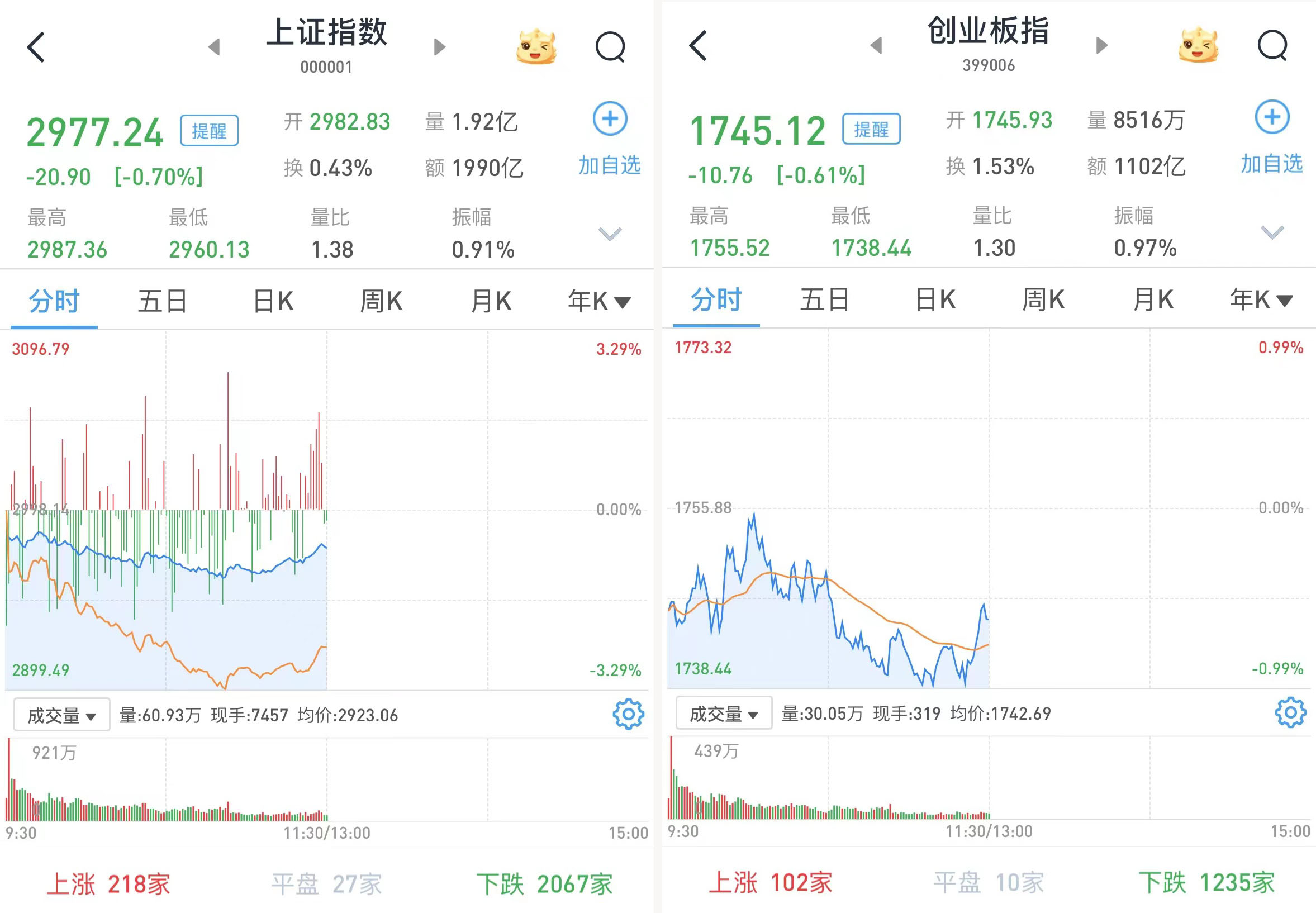 A股三大股指6月24日集体低开。进入连续竞价交易后,两市快速走低,沪指更是一度跌超1%。关键时候银行股护盘,带动两市略有回暖。从盘面上看,智慧医疗、人工智能、光伏、卫星导航、算力、锂电池、消费电子等题
...[详细]
A股三大股指6月24日集体低开。进入连续竞价交易后,两市快速走低,沪指更是一度跌超1%。关键时候银行股护盘,带动两市略有回暖。从盘面上看,智慧医疗、人工智能、光伏、卫星导航、算力、锂电池、消费电子等题
...[详细]
-
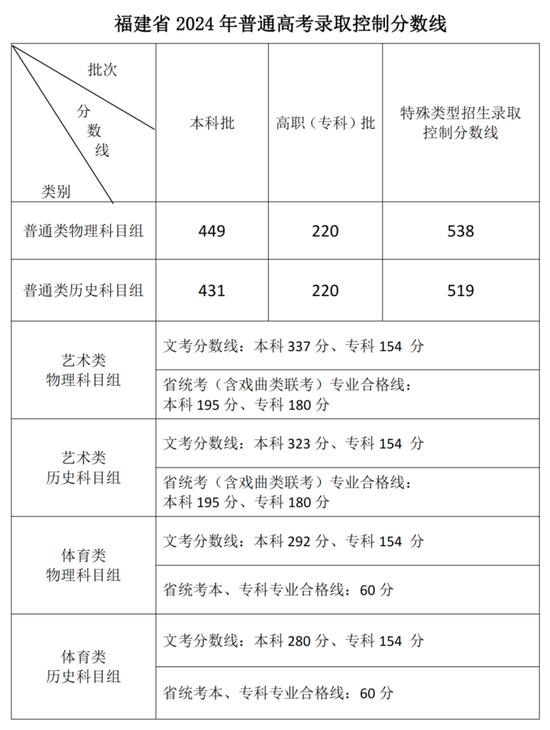 6月24日下午,福建省高等学校招生委员会召开全体会议,研究确定福建省2024年普通高考切线方案,部署高招录取工作。经会议研究决定,福建省2024年普通高考各类录取控制分数线具体如下:
...[详细]
6月24日下午,福建省高等学校招生委员会召开全体会议,研究确定福建省2024年普通高考切线方案,部署高招录取工作。经会议研究决定,福建省2024年普通高考各类录取控制分数线具体如下:
...[详细]
-
 今天13日),在中国国际经济交流中心举办的2025-2026中国经济年会上,中央财办分管日常工作的副主任、中央农办主任韩文秀表示,今年是中国式现代化进程中具有重要意义的一年,是很不平凡的一年。全年
...[详细]
今天13日),在中国国际经济交流中心举办的2025-2026中国经济年会上,中央财办分管日常工作的副主任、中央农办主任韩文秀表示,今年是中国式现代化进程中具有重要意义的一年,是很不平凡的一年。全年
...[详细]
-
 来源:环球人物 当了14年副防长的她一朝去职, 令人关注。 作者:冯璐 鲁天舒 塔季扬娜·维克托罗夫娜·舍夫佐娃下个月即将年满55周岁。她是俄罗斯军中“女一号”,官至国防部副部长,大将。不
...[详细]
来源:环球人物 当了14年副防长的她一朝去职, 令人关注。 作者:冯璐 鲁天舒 塔季扬娜·维克托罗夫娜·舍夫佐娃下个月即将年满55周岁。她是俄罗斯军中“女一号”,官至国防部副部长,大将。不
...[详细]
-
 来源:北京青年报 《青岛日报》消息,近日,致敬人民海军英雄仪式在青岛海军博物馆海军英雄广场隆重举行。海军司令员胡中明、政治委员袁华智,参谋长李汉军参加仪式,副政治委员程坚主持仪式。 该消息显示
...[详细]
来源:北京青年报 《青岛日报》消息,近日,致敬人民海军英雄仪式在青岛海军博物馆海军英雄广场隆重举行。海军司令员胡中明、政治委员袁华智,参谋长李汉军参加仪式,副政治委员程坚主持仪式。 该消息显示
...[详细]
-
 新京报贝壳财经讯 6月24日,新京报贝壳财经记者从“桂林市象山景区管理处”微信公众号获悉,受洪水影响,象鼻山景区供电设备遭受严重破坏,目前景区正在积极抢修恢复供电。为确保游客安全,象鼻山景区决定即
...[详细]
新京报贝壳财经讯 6月24日,新京报贝壳财经记者从“桂林市象山景区管理处”微信公众号获悉,受洪水影响,象鼻山景区供电设备遭受严重破坏,目前景区正在积极抢修恢复供电。为确保游客安全,象鼻山景区决定即
...[详细]
-
 L3准入车型仍有限制要求。 两款L3级有条件自动驾驶准入车型持续引起市场议论。今日,市场对两款L3准入车型的关注点聚焦在:车辆能否变道行驶?车辆限速为何有所不同? 据工信部昨日发文,长安汽车旗
...[详细]
L3准入车型仍有限制要求。 两款L3级有条件自动驾驶准入车型持续引起市场议论。今日,市场对两款L3准入车型的关注点聚焦在:车辆能否变道行驶?车辆限速为何有所不同? 据工信部昨日发文,长安汽车旗
...[详细]
-
 来源:观察者网 近日,安徽凤阳、江苏南通、湖北鄂州等地出台鼓励放弃、退出农村宅基地相关政策,引发市场关注。 据安徽省滁州市凤阳县委宣传部主办的微信公众号“中国凤阳”消息,6月20日,凤阳县房地
...[详细]
来源:观察者网 近日,安徽凤阳、江苏南通、湖北鄂州等地出台鼓励放弃、退出农村宅基地相关政策,引发市场关注。 据安徽省滁州市凤阳县委宣传部主办的微信公众号“中国凤阳”消息,6月20日,凤阳县房地
...[详细]

 硬核敞篷巴士?掷弹兵Game Viewer 2026年初量产
硬核敞篷巴士?掷弹兵Game Viewer 2026年初量产 竞彩欧洲杯|德国对阵瑞士不放水,匈牙利队赢球困难
竞彩欧洲杯|德国对阵瑞士不放水,匈牙利队赢球困难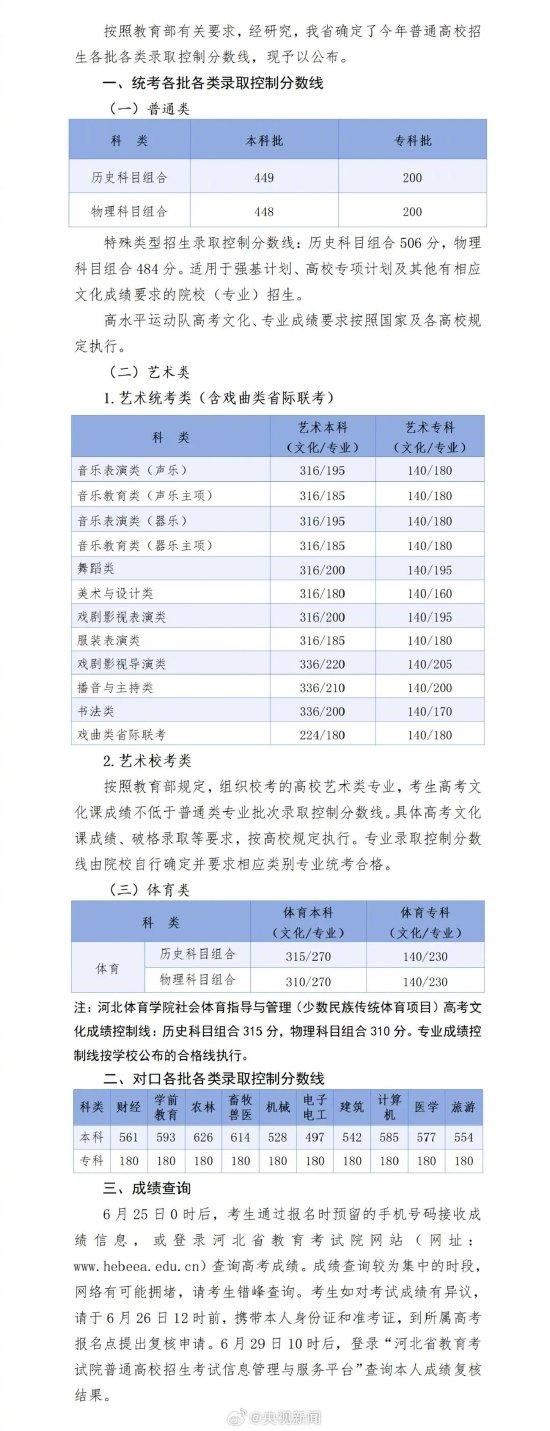 河北分数线公布扩散周知!
河北分数线公布扩散周知! 国家发改委等部门:完善县乡村三级快递物流配送体系
国家发改委等部门:完善县乡村三级快递物流配送体系 泡对养生、泡错伤身 泡温泉的正确方式你知道吗?
泡对养生、泡错伤身 泡温泉的正确方式你知道吗?
